Page 52 - 6_vip_matematik_konu

120

ALAN ÖLÇME

ÜÇGENDE YÜKSEKLİK VE ALAN

Kazanım: Üçgenin alan bağıntısını oluşturur, ilgili problemleri çözer.

Üçgende Yükseklik

P
A D

h d s
h a =c b f e
r h p
G
h e YAYINEVİ
h f
B h c =a C E d F R h r p S
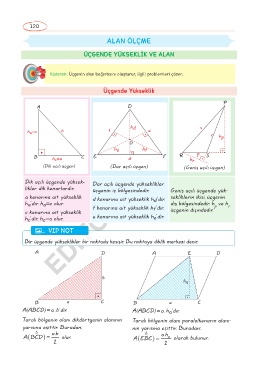
(Dik açılı üçgen) (Dar açılı üçgen) (Geniş açılı üçgen)

Dik açılı üçgende yüksek- Dar açılı üçgende yükseklikler
EDİTÖR
likler dik kenarlardır. üçgenin iç bölgesindedir. Geniş açılı üçgende yük-
a kenarına ait yükseklik d kenarına ait yükseklik h ’dir. sekliklerin ikisi, üçgenin
d
h ’dır. h =c olur. f kenarına ait yükseklik h ’dir. dış bölgesindedir. h ve h
a
a
p
r
c kenarına ait yükseklik f üçgenin dışındadır.
e
h ’dir. h =a olur. e kenarına ait yükseklik h ’dir.
c
c
W W… IIP NOT
Bir üçgende yükseklikler bir noktada kesişir. Bu noktaya diklik merkezi denir.
A D A E D

b
h a

B a C B a C
A(ABCD) = a . b’dir. A(ABCD) = a . h ’dır.
a
Taralı bölgenin alanı dikdörtgenin alanının Taralı bölgenin alanı paralelkenarın alanı-
yarısına eşittir. Buradan; nın yarısına eşittir. Buradan;
∆ a.b ∆ a.h
A (BCD ) = olur. A (EBC ) = a olarak bulunur.
2 2