Page 54 - 9-sinif-telafi

ÜÇGEN 53

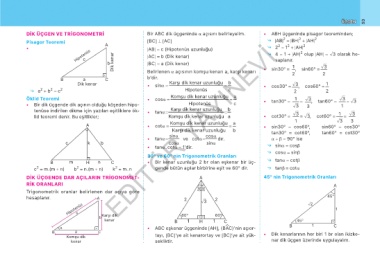
DİK ÜÇGEN VE TRİGONOMETRİ Bir ABC dik üçgeninde α açısını belirleyelim. • ABH üçgeninde pisagor teoreminden;
2
2
Pisagor Teoremi A [BC] ⊥ [AC] ⤷ |AB| = |BH| + |AH| 2
Trigonometrik oranlar belirlenen dar açıya göre İTÖR YAYINEVİ
2
2
• |AB| = c (Hipotenüs uzunluğu) ⤷ 2 = 1 + |AH| 2
Hipotenüs |AC| = b (Dik kenar) ⤷ 4 = 1 + |AH| olup |AH| = ñ3 olarak he-
2
c
saplanır.
b Dik kenar |BC| = a (Dik kenar) • sin30° = , sin60° = ñ3
1
b’dir.
B a C Belirlenen α açısının komşu kenarı a, karşı kenarı 2 2
Dik kenar • sinα = Karşı dik kenar uzunluğu b • cos30° = ñ3 , cos60° = 1
=
2
2
⤷ a + b = c 2 Hipotenüs c 2 2
Öklid Teoremi • cosα = Komşu dik kenar uzunluğu a • tan30° = 1 = ñ3 , tan60° = ñ3 = ñ3
=
• Bir dik üçgende dik açının olduğu köşeden hipo- Hipotenüs c ñ3 3 1
tenüse indirilen dikme için yazılan eşitliklere ök- • tanα = Karşı dik kenar uzunluğu b ñ3 1 ñ3
=
lid teoremi denir. Bu eşitlikler; Komşu dik kenar uzunluğu a • cot30° = 1 = ñ3, cot60° = ñ3 = 3
A • cotα = Komşu dik kenar uzunluğu a • sin30° = cos60°, sin60° = cos30°
=
Karşı dik kenar uzunluğu b tan30° = cot60°, tan60° = cot30°
sinα cosα
• tanα = ve cotα = dır. α + β = 90° ise
c k b cosα sinα
• tanα . cotα = 1’dir. ⤷ sinα = cosβ
⤷ cosα = sinβ
30° ve 60° nin Trigonometrik Oranları
B m H n C • Bir kenar uzunluğu 2 br olan eşkenar bir üç- ⤷ tanα = cotβ
2
2
2
c = m.(m + n) b = n.(m + n) k = m . n gende bütün açılar birbirine eşit ve 60° dir. ⤷ tanβ = cotα
DİK ÜÇGENDE DAR AÇILARIN TRİGONOMET- A 45° nin Trigonometrik Oranları
RİK ORANLARI 30° 30° A
hesaplanır. A Karşı dikED 2 ñ3 2 45°
Hipotenüs ñ2 1
c
b 60° 60°
kenar B 1 H 1 C 45°
α • ABC eşkenar üçgeninde [AH], (BëAC)’nin açıor- B 1 C
B a C • Dik kenarlarının her biri 1 br olan ikizke-
Komşu dik tayı, [BC]’ye ait kenarortay ve [BC]’ye ait yük-
kenar sekliktir. nar dik üçgen üzerinde uygulayalım.