Page 16 - 9. SINIF MATEMATİK FAVORİ DEFTERİM

ÖZETİN ÖZETİ 1. Ünite: Mantık

Koşullu Önerme ve İki Yönlü Koşullu Önerme

ise" Bağlacı ile Oluşan Bileşik Önermeler
Q p ve q önermelerinin "ise" bağlacı kullanılarak birleştirilmesiyle oluşan bileşik önermeye koşullu önerme denir. Koşullu önermeler
p ⇒ q şeklinde gösterilip "p ise q" şeklinde okunur.

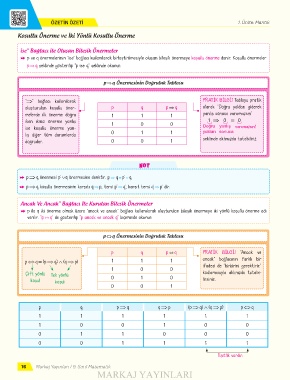
p  q Önermesinin Doğruluk Tablosu

"" bağlacı kullanılarak PRATİK BİLGİ! Tabloyu pratik
oluşturulan koşullu öner- p q p  q olarak "Doğru yoldan giderek
melerde ilk önerme doğru 1 1 1 yanlış sonuca varamazsın"
iken ikinci önerme yanlış 1 0 0 1  0 ≡ 0
ise koşullu önerme yan- Doğru yanlış varamazsın!
yoldan sonuca
lış diğer tüm durumlarda 0 1 1
doğrudur. 0 0 1 şeklinde aklımızda tutabiliriz.

NOT

Q p  q önermesi p' ∨q önermesine denktir. p ⇒ q ≡ p' ∨ q

Q p  q koşullu önermesinin karşıtı q ⇒ p, tersi p' ⇒ q', karşıt tersi q' ⇒ p' dir.

Ancak Ve Ancak" Bağlacı İle Kurulan Bileşik Önermeler
Q p ile q iki önerme olmak üzere "ancak ve ancak" bağlacı kullanılarak oluşturulan bileşik önermeye iki yönlü koşullu önerme adı
verilir. "p ⇔ q" ile gösterilip "p ancak ve ancak q" biçiminde okunur.

p ⇔⇔ q Önermesinin Doğruluk Tablosu

p q p ⇔ q PRATİK BİLGİ! "Ancak ve
p ⇔ q ≡ (p ⇒ q) ∧ (q ⇒ p) 1 1 1 ancak" bağlacının farklı bir
ifadesi de "birbirini gerektirir."
1 0 0
Çift yönlü Tek yönlü kodlamasıyla aklınızda tutabi-
koşul koşul 0 1 0 lirsiniz.
0 0 1

p q p ⇒ q q ⇒ p (p ⇒ q) ∧ (q ⇒ p) p ⇔ q

1 1 1 1 1 1
1 0 0 1 0 0
0 1 1 0 0 0
0 0 1 1 1 1

Eşitlik vardır.

16 Markaj Yayınları / 9. Sınıf Matematik
MARKAJ YAYINLARI