Page 31 - 9. SINIF MATEMATİK FAVORİ DEFTERİM

2. Ünite: Kümeler ÖZETİN ÖZETİ

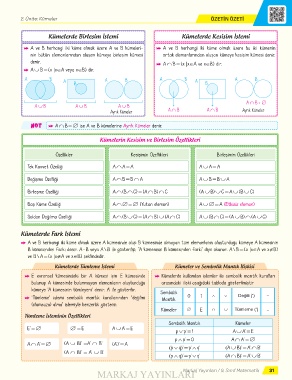
Kümelerde Birleşim İşlemi Kümelerde Kesişim İşlemi

Q A ve B herhangi iki küme olmak üzere A ve B kümeleri- Q A ve B herhangi iki küme olmak üzere bu iki kümenin
nin bütün elemanlarından oluşan kümeye birleşim kümesi ortak elemanlarından oluşan kümeye kesişim kümesi denir.
denir.
Q A ∩ B = {x |x∈A ve x∈B} dir.
Q A ∪ B = {x |x∈A veya x∈B} dir.
A B A B A B
A B A B A B

A ∩ B = ∅
A ∪ B A ∪ B A ∪ B
Ayrık Kümeler A ∩ B A ∩ B Ayrık Kümeler

NOT Q A ∩ B = ∅ ise A ve B kümelerine Ayrık Kümeler denir.

Kümelerin Kesişim ve Birleşim Özellikleri

Özellikler Kesişimin Özellikleri Birleşimin Özellikleri

Tek Kuvvet Özelliği A ∩ A = A A ∪ A = A

Değişme Özelliği A ∩ B = B ∩ A A ∪ B = B ∪ A

Birleşme Özelliği A ∩ (B ∩ C) = (A ∩ B) ∩ C (A ∪ B) ∪ C = A ∪ (B ∪ C)

Boş Küme Özelliği A ∩ ∅ = ∅ (Yutan eleman) A ∪ ∅ = A (Etkisiz eleman)

Soldan Dağılma Özelliği A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C) A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C)

Kümelerde Fark İşlemi

Q A ve B herhangi iki küme olmak üzere A kümesinde olup B kümesinde olmayan tüm elemanların oluşturduğu kümeye A kümesinin
B kümesinden farkı denir. A - B veya A \ B ile gösterilip, "A kümesinin B kümesinden farkı" diye okunur. A \ B = {x |x∈A ve x∉B}
ve B \ A = {x |x∉A ve x∈B} şeklindedir.

Kümelerde Tümleme İşlemi Kümeler ve Sembolik Mantık İlişkisi

Q E evrensel kümesindeki bir A kümesi için E kümesinde Q Kümelerde kullanılan işlemler ile sembolik mantık kuralları
bulunup A kümesinde bulunmayan elemanların oluşturduğu arasındaki ilişki aşağıdaki tabloda gösterilmiştir
kümeye "A kümesinin tümleyeni" denir. A' ile gösterilir.
Sembolik
Q "Tümleme" işlemi sembolik mantık kurallarından "değilini Mantık 0 1 ∧ ∨ Değili (') ≡
(olumsuzu) alma" işlemiyle benzerlik gösterir.
Kümeler ∅ E ∩ ∪ Tümleme (') =
Tümleme İşleminin Özellikleri
Sembolik Mantık Kümeler
E' = ∅ ∅' = E A ∪ A' = E
p ∨ p' ≡ 1 A ∪ A' ≡ E
p ∧ p' ≡ 0 A ∩ A' = ∅
A ∩ A' = ∅ (A ∪ B)' =A' ∩ B' (A')' = A
(p ∨ q)' ≡ p' ∧ q' (A ∪ B)' = A' ∩ B'
(A ∩ B)' = A' ∪ B'
(p ∧ q)' ≡ p' ∨ q' (A ∩ B)' = A' ∪ B'

Markaj Yayınları / 9. Sınıf Matematik
MARKAJ YAYINLARI 31