Page 37 - 10_Matematik_ogretmenin

FONKSİYONLAR 35

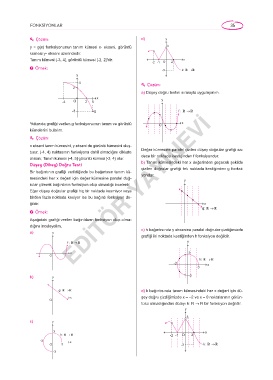
˜ Çözük: d) y
y = g(x) fonksiyonunun tanım kümesi x- ekseni, görüntü 3
kümesi y- ekseni üzerindedir.
Tanım kümesi (-3, 4], görüntü kümesi [-2, 2]'dir. x
-2 -1 O 2
p Örnek: -3 k: →
y
4 ˜ Çözük:
2
a) Düşey doğru testini sırasıyla uygulayalım.
x
-4 O 2 5 y

-3 g f : →

Yukarıda grafiği verilen g fonksiyonunun tanım ve görüntü O x
kümelerini bulalım.
˜ Çözük:
x ekseni tanım kümesini, y ekseni de görüntü kümesini oluş-
turur. (-4, 4) noktasının fonksiyona dahil olmadığını dikkate Değer kümesine paralel çizilen düşey doğrular grafiği sa-
dece bir noktada kestiğinden f fonksiyondur.
alırsak; Tanım kümesi (-4, 5] görüntü kümesi [-3, 4) olur. YAYINEVİ
Düşry (Dnkry) DoÖğu Trsen b) Tanım kümesindeki her x değerinden geçecek şekilde
çizilen doğrular grafiği tek noktada kestiğinden g fonksi-
Bir bağıntının grafiği verildiğinde bu bağıntının tanım kü- yondur.
mesindeki her x değeri için değer kümesine paralel doğ- y
rular çizerek bağıntının fonksiyon olup olmadığı incelenir.
Eğer düşey doğrular grafiği hiç bir noktada kesmiyor veya
birden fazla noktada kesiyor ise bu bağıntı fonksiyon de-
ğildir. x
g: →
p Örnek:
Aşağıdaki grafiği verilen bağıntıların fonksiyon olup olma-
dığını inceleyelim. EDİTÖR
a) y c) h bağıntısında y eksenine paralel doğrular çizdiğimizde
grafiği iki noktada kestiğinden h fonksiyon değildir.
f : → y

x 3
O
h: →
-3 x
3
b) y -3

g: → d) k bağıntısında tanım kümesindeki her x değeri için dü-
x şey doğru çizdiğimizde x = -2 ve x = 0 noktalarının görün-
O
tüsü olmadığından dolayı k: R → R bir fonksiyon değildir.
y

3
c) y

3 x
h: → -2 -2 -1 O 2
-3 x
O 3 -3 k: →
-3