Page 105 - 10_Matematik_ogretmenin

DÖRTGENLER VE ÇOKGENLER 103

p Örnek: p Örnek:
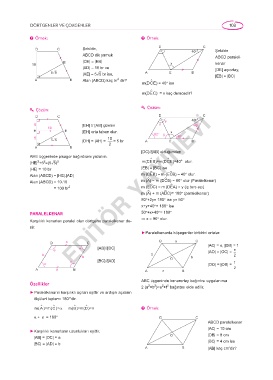
D C Şekilde, D 40 o C Şekilde
ABCD dik yamuk ABCD paralel-
E |CE| = |EB| kenar
10 x
|AD| = 10 br ve [DE] açıortay,
5ñ5 |AE| = 5ñ5 br ise, A E B |EB| = |BC|
2
A B Alan (ABCD) kaç br dir? ∧
m(DCE) = 40° ise
∧
m(DEC) = x kaç derecedir?

˜ Çözük: ˜ Çözük:
D C D C
y 40 o
5 10 [EH] // [AB] çizelim y 40 o
H E [EH] orta taban olur. 80 o x
5 5ñ5 |DH| = |AH| = 10 = 5 br y 40 o
2 A E B
A B
[DC]//[AB] olduğundan
AHE üçgeninde pisagor bağıntısını yazalım. YAYINEVİ
∧
∧
2
2
|HE| +5 =(5ñ5) 2 m(CEB)=m(DCE)=40 o olur.
|HE| = 10 br |EB| = |BC| ise
Alan (ABCD) = |HE|.|AD| m (CëEB) = m (EëCB) = 40° olur.
Alan (ABCD) = 10.10 m (ëA) = m (DëCB) = 80° olur (Paralelkenar)
EDİTÖR
= 100 br 2 m (EëDC) = m (DëEA) = y (iç ters açı)
m (ëA) + m (AëDC)= 180° (paralelkenar)
80°+2y= 180° ise y= 50°
x+y+40°= 180° ise
PARALELKENAR 50°+x+40°= 180°
⇒ x = 90° olur.
Karşılıklı kenarları paralel olan dörtgene paralelkenar de-
nir.
► Paralelkenarda köşegenler birbirini ortalar.

D a C D a C |AC| = e, |DB| = f
α [AB]//[DC]
θ |AO| = |OC| = e
b b 2
b O b
θ [BC]//[AD] f
α |DO| = |OB| =
A a B A a B 2

ABC üçgeninde kenarortay bağıntısı uygulanırsa
zraankarğ
2
2
2
2
2 (a +b )=e +f bağıntısı elde edilir.
► Paralelkenarın karşılıklı açıları eşittir ve ardışık açıların
ölçüleri toplamı 180°’dir.
∧ ∧ ∧ ∧
m( A )=m(C)= α m(B)=m(D)= θ p Örnek:
α + θ = 180° D C
ABCD paralelkenar
|AC| = 10 cm
► Karşılıklı kenarların uzunlukları eşittir.
|AB| = |DC| = a O |DB| = 8 cm
|BC| = |AD| = b |BC| = 4 cm ise
A B |AB| kaç cm’dir?