Page 106 - 10_Matematik_ogretmenin

104 DÖRTGENLER VE ÇOKGENLER

˜ Çözük: ► Paralelkenarda iç açılara ait açıortaylar bir dikdörtgen
oluşturur.
D C
D C
4 5
K
5 O 4 4 T F

E
A x B
A B
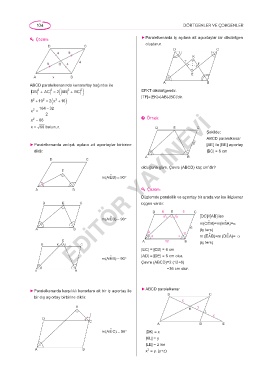
ABCD paralelkenarında kenarortay bağıntısı ile
DB + 2 AC = 2 2 AB + ( 2 BC 2 ) EFKT dikdörtgendir.
8 + 2 10 = 2 ( 2 x + 2 16 ) |TF|=|EK|=|AB|-|BC|’dir.
2
x = 164 32−
YAYINEVİ
2
2
x = 66 p Örnek:
x = 66 bulunur. D E C
Şekilde:
ABCD paralelkenar
► Paralelkenarda ardışık açılara ait açıortaylar birbirine 6 [AE] ile [BE] açıortay
diktir. |BC| = 6 cm
A B
D C
olduğuna göre, Çevre (ABCD) kaç cm’dir?
E
∧
m(AEB) = 90 °
EDİTÖR
A B ˜ Çözük:
Düzlemde paralellik ve açıortay bir arada var ise ikizkenar
D E C üçgen vardır.

D 6 E 6 C
∧ θ α [DC]//[AB] ise
m(AEB) = 90 ° ∧ ∧
m(CEB)=m(EBA)=α
A B 6 (iç ters)
θ α ∧ ∧
θ α m (EAB)=m (DEA)= θ
E A 12 B (iç ters)
D K L C
|EC| = |CB| = 6 cm
∧ |AD| = |DE| = 6 cm olur.
m(AEB) = 90 °
Çevre (ABCD)=2 (12+6)
=36 cm olur.
A B

► Paralelkenarda karşılıklı kenarlara ait bir iç açıortay ile ► ABCD paralelkenar
bir dış açıortay birbirine diktir. D C
x
E K y
L
z
D
C
A B E
∧
m(AEC) = 90 ° |DK| = x
|KL| = y
|LE| = z ise
A B x = y. (y+z)
2