Page 101 - 10_Matematik_ogretmenin

DÖRTGENLER VE ÇOKGENLER 99

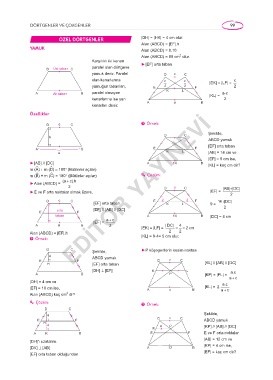
ÖZEL DÖRTGENLER |DH| = |HK| = 4 cm olur.
Alan (ABCD) = |EF|.h
YAMUK Alan (ABCD) = 8.10
2
Alan (ABCD) = 80 cm olur.
Karşılıklı iki kenarı
paralel olan dörtgene ► [EF] orta taban
D Üst taban C
yamuk denir. Paralel D c C
olan kenarlarına c c |EK| = |LF| = c
yamuğun tabanları, E 2 2 F 2
A Alt taban B paralel olmayan K L |KL| = a-c
kenarlarına ise yan 2
kenarları denir. A a B
zraankarğ

D c C p Örnek:

h D C Şekilde,
ABCD yamuk
[EF] orta taban
A B E K L F
a YAYINEVİ |AB| = 14 cm ve
|EF| = 9 cm ise,
► [AB] // [DC] A 14 B |KL| = kaç cm dir?
m (ëA) + m (ëD) = 180° (Bütünler açılar)
m (ëB) + m (ëC) = 180° (Bütünler açılar) ˜ Çözük:
(a c).h+
► Alan (ABCD) =
2 D 4 C |AB| |DC|+
► E ve F orta noktalar olmak üzere, |EF| = 2

D c C E 2 2 F 14 |DC|+
[EF] orta taban K L 9 = 2
E orta F [EF] // [AB] // [DC]
taban A 14 B |DC| = 4 cm
|EF| = ac+
2
B
A a EDİTÖR |DC | 4
|EK| = |LF| = = = 2 cm
2
Alan (ABCD) = |EF|.h |KL| = 9-4= 5 cm olur. 2
p Örnek:
D C Şekilde, ► P köşegenlerin kesim noktası
4 ABCD yamuk
E F D c C [KL] // [AB] // [DC]
H [EF] orta taban
[DH] ⊥ [EF] K L
A B P |KP| = |PL| = a.c
ac+
|DH| = 4 cm ve a.c
|EF| = 10 cm ise, A a B |KL| = 2. ac+
2
Alan (ABCD) kaç cm dr?
˜ Çözük:
p Örnek:
D C
4 Şekilde,
E F D c C ABCD yamuk
H 4
K 4 P [KP] // [AB] // [DC]
A K B E F E ve F orta noktalar
|AB| = 12 cm ve
[DH]'ı uzatalım.
[DK] ⊥ [AB] A 12 B |KP| = 4 cm ise,
[EF] orta taban olduğundan |EF| = kaç cm dir?