Page 99 - 10_Matematik_ogretmenin

DÖRTGENLER VE ÇOKGENLER 97

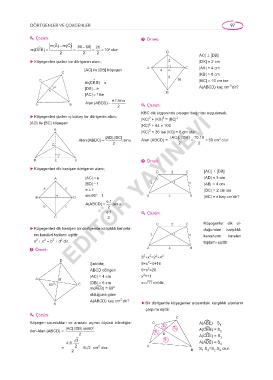
˜ Çözük: p Örnek:

m(A) −m(C) 80 − 60 20

m(DEK) = = = = 10 olur.
°
2 2 2 D
AC] ⊥ [DB]
► Köşegenleri çizilen bir dörtgenin alanı; 2 |DK| = 2 cm
[AC] ile [DB] köşegen A 4 K C |AK| = 4 cm
C |KB| = 8 cm
8
∧
D m(CKB) = α 10 |BC| = 10 cm ise
2
α |DB| = e A(ABCD) kaç cm ’dir?
K B
|AC| = f ise
e.f.sin α
A B Alan (ABCD) = 2 ˜ Çözük:
KBC dik üçgeninde pisagor bağıntısı uygularsak;
► Köşegenleri çizilen iç bükey bir dörtgenin alanı; |KC| + |KB| = |BC| 2
2
2
[AD] ile [BC] köşegen
2
|KC| + 64 = 100
A
2
|KC| = 36 ise |KC| = 6 cm olur.
|AD|.|BC| | AC |.|DB | 10.10
2
Alan (ABDC) = .sinα Alan (ABCD) = = = 50 cm olur.
D 2 2 2
α YAYINEVİ
B E C p Örnek:
► Köşegenleri dik kesişen dörtgenin alanı;
D 2 C [AC] ⊥ [DB]
A |AC| = e |AD| = 3 cm
EDİTÖR
|BD| = f 3 x |AB| = 4 cm
a d e ⊥ f |DC| = 2 cm ise
B D sin 90 °= 1 A 4 B |BC| = x kaç cm’dir?
e.f
A(ABCD) = .sin α
b c 2
e.f Çözük:
= ˜
C 2
D 2 C Köşegenler dik ol-
► Köşegenleri dik kesişen bir dörtgende karşılıklı kenarla- duğundan karşılıklı
rın kareleri toplamı eşittir. 3 x kenarların kareleri
2
2
2
2
a + c = b + d dir. toplamı eşittir.
p Örnek: A 4 B
2
2
2
3 +x =2 +4 2
D
2
Şekilde; 9+x =4+16
2
ABCD dörtgen 9+x =20
2
|AC| = 4 cm x =11
A E
60 o C |DB| = 6 cm x=ò11 cm'dir.
m(AéEB) = 60 o
olduğuna göre
2
A(ABCD) kaç cm ’dir?
B ► Bir dörtgende köşegenler arasındaki karşılıklı alanların
çarpımı eşittir.
˜ Çözük:
C
Köşegen uzunlukları ve aradaki açının ölçüsü bilindiğin- D A(A¿BE) = S 1
|AC|.|DB|.sin60° S 3 S A(C¿EB) = S
den Alan (ABCD) = S 2 2
2 4 E A(C¿DE) = S
3 S 1 3
4.6. A(A¿DE) = S 4
2
= 2 = 63 cm olur. A S .S =S .S olur.
2 B 1 3 2 4