Page 26 - DGS HIZLI KONU ANLATIMLI - DATA YAYINLARI

D
DÖRTGENLER VE ÖZEL DÖRTGENLERÖRTGENLER VE ÖZEL DÖRTGENLER 5. BÖLÜM 11919
1

* Doğrusal olmayan dört noktanın ikişer ikişer ÖZEL DÖRTGENLERDE ÇEVRE VE ALAN HESAP-
birleştirilmesi ile oluşturulan geometrik şekle LAMALARI
dörtgen denir.

o
* Dörtgenin iç açılarının toplamı 360 dir. 1. KARE
o
* Dörtgenin dış açılarının toplamı 360 dir. A a D
Ç(ABCD) = 4a
Dikka a a A(ABCD) = a 2
Dikkat!t!
DATA YAYINLARI
A D
B a C

E a

B C 2. DİKDÖRTGEN
m(ëA) + m(ëB) b
a = A D
2
Ç(ABCD) = 2(a+b)
a a
œ Örnek: A D A(ABCD) = a.b

80 o B b C
E
x
3. EŞKENAR DÖRTGEN
B C
A
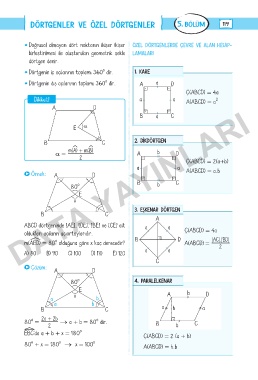
ABCD dörtgeninde [AE], [DE], [BE] ve [CE] ait a a
oldukları açıların açıortaylarıdır. Ç(ABCD) = 4a
o
m(AéED) = 80 olduğuna göre x kaç derecedir? B D A(ABCD) = |AC|.|BD|
2
a a
A) 80 B) 90 C) 100 D) 110 E) 120
C
œ Çözüm:
A D
80 o 4. PARALELKENAR
E b
a x b A D
a b
B C a h a

o
o
80 = 2a + 2b → a + b = 80 dir. B C
2 b
o
EÿBC'de a + b + x = 180 Ç(ABCD) = 2 (a + b)
o
o
o
80 + x = 180 → x = 100 A(ABCD) = h.b