Page 123 - 10. SINIF VIP TÜM DERSLER KONU ANLATIMLI - EDİTÖR YAYINLARI

ÖZEL DÖRTGENLER (DEL
ÖZEL DÖRTGENLER (DELTOID)TOID) 5. ÜNITE 123
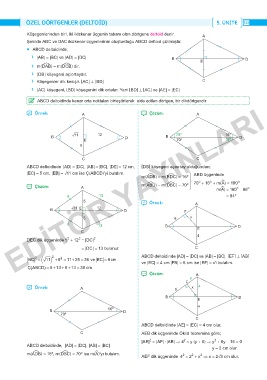
Köşegenlerinden biri, iki ikizkenar üçgenin tabanı olan dörtgene deltoid denir. A
Şekilde ABC ve DAC ikizkenar üçgenlerinin oluşturduğu ABCD deltoid çizilmiştir.
• ABCD deltoidinde;
› |AB| = |BC| ve |AD| = |DC| B
E D
› m(DéAB) = m(DéCB) dir.

› [DB] köşegeni açıortaydır.
› Köşegenler dik kesişir. [AC] ⊥ [BD] C

› [AC] köşegeni, [BD] köşegenini dik ortalar. Yani [BD] ⊥ [AC] ve |AE| = |EC|

{ ABCD deltoidinde kenar orta noktaları birleştirilerek elde edilen dörtgen, bir dikdörtgendir.
EDİTÖR YAYINLARI
̛ Örnek: A ̚ Çözüm: A

B ò11 12 D B 70º 16º D
E 70º 16º
5

C C
ABCD deltoidinde |AD| = |DC|, |AB| = |BC|, |DE| = 12 cm, [DB] köşegeni açıortay olduğundan;
|EC| = 5 cm, |EB| = ò11 cm ise Ç(ABCD)'yi bulalım. ABD üçgeninde
m(AéDB) = m(BéDC) = 16º
o
o
o
̚ Çözüm: A m(AéBD) = m(DéBC) = 70º 70 + 16 + m(ëA) = 180
o
o
m(ëA) = 180 - 86
6 13 = 94º
5
̛ Örnek: A
B ò11 E 12 D F
5 6 x
6 13 B D
C E
4
2
2
2
DEC dik üçgeninde 5 + 12 = |DC|
= |DC| = 13 bulunur. C
2 2 2 ABCD deltoidinde |AD| = |DC| ve |AB| = |BC| [EF]  [AB]
= BC ( ) +11 = 5 + 11 25 = 36 ve = BC 6cm ve |EC| = 4 cm |FB| = 6 cm ise |EF| = x'i bulalım.
Ç(ABCD) = +6 13 ++6 13 = 38 cm
̚ Çözüm: A
y
F
̛ Örnek: A 6 x 4
B D
E
4
B 16º D
70º
C
ABCD deltoidinde |AE| = |EC| = 4 cm olur.
C AEB dik üçgeninde Öklid teoremine göre;
.
2
2
2
|AE| = |AF| |AB| ⇒ 4 = y (y + 6) ⇒ y + 6y - 16 = 0
ABCD deltoidinde, |AD| = |DC|, |AB| = |BC|
y = 2 cm olur.
m(AéDB) = 16º, m(DéBC) = 70º ise m(ëA)'yı bulalım.
2
2
2
AEF dik üçgeninde 4 = 2 + x ⇒ x = 2ñ3 cm olur.