Page 121 - 10. SINIF VIP TÜM DERSLER KONU ANLATIMLI - EDİTÖR YAYINLARI

ÖZEL DÖRTGENLER (KARE)
ÖZEL DÖRTGENLER (KARE) 5. ÜNITE 121
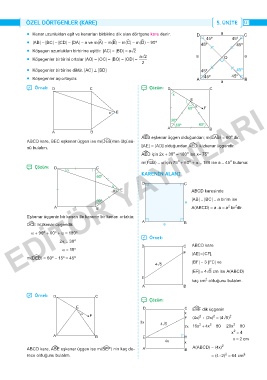
• Kenar uzunlukları eşit ve kenarları birbirine dik olan dörtgene kare denir. D a C
• |AB| = |BC| = |CD| = |DA| = a ve m(ëA) = m(ëB) = m(ëC) = m(ëD) = 90º 45º 45º 45º 45º
• Köşegen uzunlukları birbirine eşittir. |AC| = |BD| = añ2
• Köşegenler birbirini ortalar |AO| = |OC| = |BO| = |OD| = añ2 a O a
2
• Köşegenler birbirine diktir. [AC]  [BD] 45º 45º
• Köşegenler açıortaydır. A 45º a 45º B

̛ Örnek: D C ̚ Çözüm: D C
x
E
EDİTÖR YAYINLARI
60º α F
x E
30º
60º 60º
A B
A B
o
A¿EB eşkenar üçgen olduğundan; m(EéAB) = 60 dir.
ABCD kare, BEC eşkenar üçgen ise m(DéEB)'nın ölçüsü-
nü bulalım. [AE] = [AD] olduğundan A¿ED ikizkenar üçgendir.
o
o
A¿ED için 2x + 30 = 180 ise x= 75 o
o
o
o
m(FéEB) = a için 75 + 60 + a = 180 ise a = 45 bulunur.
̚ Çözüm: D α C
60º KARENIN ALANI
D C
α
x E ABCD karesinde
60º a |AB| = |BC| = a birim ise
2
2
A B A(ABCD) = a � a = a br dir.
Eşkenar üçgenin bir kenarı ile karenin bir kenarı ortaktır.
A B
D¿CE ikizkenar üçgendir. a
a + 90º + 60º + a = 180º
̛ Örnek:
2a = 30º
D C ABCD kare
a = 15º
F |AE| = |CF|,
m(DéEB) = 60º - 15º = 45º
4ñ5 |BF| = 3 |FC| ve
|EF| = 4ñ5 cm ise A(ABCD)
E
2
kaç cm olduğunu bulalım.
A B
̛ Örnek: D C
̚ Çözüm:
E D C E¿HF dik üçgenin
α F x F (4x) + (2x) = (4ñ5) 2
2
2
3x 4ñ5
2
2
2
2x 16x + 4x = 80 20x = 80
2
x = 4
A B E H
4x x x = 2 cm
2
ABCD kare, A¿BE eşkenar üçgen ise m(BéEF) nin kaç de- A B A(ABCD) = (4x)
2
rece olduğunu bulalım. = (4 . 2) = 64 cm 2