Page 141 - 9_Matematik_ogretmenin

ÜÇGENLER 139

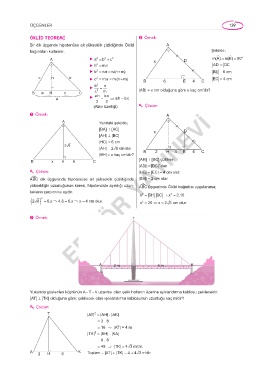
ÖKLİD TEOREMİ p Örnek:
Bir dik üçgende hipotenüse ait yükseklik çizildiğinde Öklid A
bağıntıları kullanılır. Şekilde;

2
2
A ► a = b + c 2 x D m(A) = m(E) = 90 o
2
► h = m.n AD = DC
2
► b = n.a = n.(n m)+ BE = 6 cm
c h b ► c = m.a = m.(n m)+ B 6 E 4 C EC = 4 cm
2
b 2 n
► 2 = |AB| = x cm olduğuna göre x kaç cm’dir?
B m H n C c a.h m
b.c
=
a ► = ⇒ a.h b.c
2 2
(Alan özelliği) ˜ Çözük:
p Örnek: A
A Yandaki şekilde;
[BA] ⊥ [AC] x D
[AH] ⊥ [BC]
|HC| = 6 cm
2 6
|AH| = 2ñ6 cm ise B 2 H 4 E 4 C
|BH| = x kaç cm'dir? YAYINEVİ
[AH] ⊥ [BC] çizilirse;
B x H 6 C
|AD| = |DC|’ den
˜ Çözük: |HE| = |EC| = 4 cm olur.
A¿BC dik üçgeninde hipotenüse ait yükseklik çizildiğinde |BH| = 2 cm olur.
yüksekliğin uzunluğunun karesi, hipotenüste ayırdığı uzun- A¿BC üçgeninde Öklid bağıntısı uygulanırsa;
lukların çarpımına eşittir. 2 BH . BC ⇒ x = 2 2.10
EDİTÖR x =
2
( 2 6 ) = 6.x ⇒ 4.6 = 6.x ⇒ x = 4 cm olur. x = 2 20 ⇒ x = 2 5 cm olur.

p Örnek: T

K
A
6 m
2 m

Yukarıda gösterilen köprünün A - T - K uzantısı olan çelik hatların üzerine ışıklandırma kablosu çekilecektir.
[AT] ⊥ [TK] olduğuna göre; çekilecek olan ışıklandırma kablosunun uzunluğu kaç m'dir?

˜ Çözük:
T |AT| = |AH| . |AK|
2
= 2 . 8
= 16 ⇒ |AT| = 4 m
2
|TK| = |KH| . |KA|
= 6 . 8
= 48 ⇒ |TK| = 4ñ3 m'dir.
A 2 H 6 K Toplam = |AT| + |TK| = 4 + 4ñ3 m'dir.