Page 131 - 10. SINIF VIP TÜM DERSLER KONU ANLATIMLI - EDİTÖR YAYINLARI

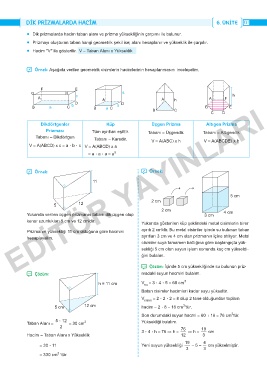
DIK PRIZMALARDA HACIM
DIK PRIZMALARDA HACIM 6. ÜNITE 131
• Dik prizmalarda hacim taban alanı ve prizma yüksekliğinin çarpımı ile bulunur.
• Prizmayı oluşturan taban hangi geometrik şekil ise; alanı hesaplanır ve yükseklik ile çarpılır.
• Hacim "V" ile gösterilir. V = Taban Alanı x Yükseklik

̛ Örnek: Aşağıda verilen geometrik cisimlerin hacimlerinin hesaplanmasını inceleyelim.

F E
G H c a h
A A A h A F
EDİTÖR YAYINLARI
B a C b D B a C a D B E
B C
C D

Dikdörtgenler Küp Üçgen Prizma Altıgen Prizma
Prizması Tüm ayrıtları eşittir. Tabanı = Üçgendir. Tabanı = Altıgendir.
Tabanı = Dikdörtgen Tabanı = Karedir.
V = A(ABCD) x c = a . . V = A(ABC) x h V = A(ABCDE) x h
b c V = A(ABCD) x a
= a . . 3
a a = a

̛ Örnek: ̛ Örnek:

11

5 cm
2 cm
5 12
2 cm
Yukarıda verilen üçgen prizmanın tabanı dik üçgen olup 3 cm 4 cm
kenar uzunlukları 5 cm ve 12 cm'dir. Yukarıda gösterilen küp şeklindeki metal cisimlerin birer

Prizmanın yüksekliği 11 cm olduğuna göre hacmini ayrıtı 2 cm'dir. Bu metal cisimler içinde su bulunan taban
hesaplayalım. ayrıtları 3 cm ve 4 cm olan prizmanın içine atılıyor. Metal
cisimler suya tamamen battığına göre başlangıçta yük-
sekliği 5 cm olan suyun işlem sonunda kaç cm yükseldi-
ğini bulalım.

̚ Çözüm: Içinde 5 cm yüksekliğinde su bulunan priz-
̚ Çözüm: madaki suyun hacmini bulalım.
. .
h = 11 cm V = 3 4 5 = 60 cm 3
su
Batan cisimler hacimleri kadar suyu yükseltir.
. .
V cisim = 2 2 2 = 8 olup 2 tane olduğundan toplam
.
3
5 cm 12 cm hacim = 2 8 = 16 cm 'tür.
3
.
5 12 Son durumdaki suyun hacmi = 60 + 16 = 76 cm tür.
Yüksekliği bulalım.
Taban Alanı = = 30 cm 2
2 3 . . 76 19
Hacim = Taban Alanı x Yükseklik 4 h = 76 ⇒ h = 12 ⇒ h = 3 cm
= 30 . 11 Yeni suyun yüksekliği 19 - 5 = 4 cm yükselmiştir.
3 3
3
= 330 cm 'tür.