Page 37 - 10_matematik_ogretmenin

DÖRTGENLER VE ÇOKGENLER 5. ÜNİTE 92

ÇOKGENLER
ÇOKGENİN AÇILARI
)
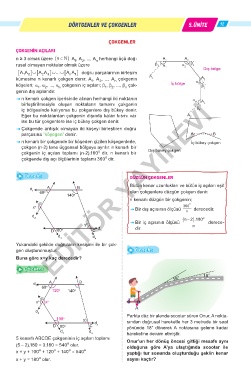
n ≥ 3 olmak üzere (n∈ A , A , ..., A herhangi üçü doğ- A 1 A 2
1
2
n
rusal olmayan noktalar olmak üzere β 1 α 1 α 2 β 2
AA AA ... AA doğru parçalarının birleşim Dış bölge
2
12
3
1
n
kümesine n kenarlı çokgen denir. A , A , ..., A çokgenin A n α A 3
2
1
n
köşeleri; α , α , ..., α çokgenin iç açıları; β , β , ..., β çok- İç bölge 3 β 3
2
n
1
n
2
1
genin dış açılarıdır.
ˇ n kenarlı çokgen içerisinde alınan herhangi iki noktanın α A
birleştirilmesiyle oluşan noktaların tamamı çokgenin 4 4
iç bölgesinde kalıyorsa bu çokgenlere dış bükey denir. β 4
Eğer bu noktalardan çokgenin dışında kalan kısmı var A 5
ise bu tür çokgenlere ise iç bükey çokgen denir.
ˇ Çokgende ardışık olmayan iki köşeyi birleştiren doğru
parçasına “köşegen” denir. A B
ˇ n kenarlı bir çokgende bir köşeden çizilen köşegenlerle, İç bükey çokgen
çokgen (n-2) tane üçgensel bölgeye ayrılır. n kenarlı bir
o
çokgenin iç açıları toplamı (n-2).180 dir. n kenarlı bir Dış bükey çokgen
o
çokgende dış açı ölçülerinin toplamı 360 dir.
Örnek: DÜZGÜN ÇOKGENLER
Bütün kenar uzunlukları ve bütün iç açıları eşit
B
d A EDİTÖR YAYINEVİ
1 60 o olan çokgenlere düzgün çokgen denir.
140 o
n kenarlı düzgün bir çokgenin;
E o
x o 360
ˇ Bir dış açısının ölçüsü n derecedir.
d
2 (n 2− ).180 o
y o ˇ Bir iç açısının ölçüsü n derece-
D 80 o C d 5 dir.
d 3 d 4
Yukarıdaki şekilde doğruların kesişimi ile bir çok-
gen oluşturulmuştur. Örnek:
Buna göre x+y kaç derecedir?
Çözüm:
18° 18°
d A B
1 60 o
120 o 140 o
E
x o x o
A
d 2
100 o y o Parkta düz bir alanda scooter süren Onur, A nokta-
sından doğrusal hareketle her 3 metrede bir saat
D 80 o C d 5 yönünde 18° dönerek A noktasına gelene kadar
d 3 d 4 hareketine devam etmiştir.
5 kenarlı ABCDE çokgeninin iç açıları toplamı Onur’un her dönüş öncesi gittiği mesafe aynı
o
(5 – 2).180 = 3.180 = 540 olur. olduğuna göre A’ya ulaştığında scooter ile
o
o
o
x + y + 100 + 120 + 140 = 540 o yaptığı tur sonunda oluşturduğu şeklin kenar
o
x + y = 180 olur. sayısı kaçtır?