Page 29 - tyt-tum-dersler-konu

BÖLÜM

5 ÇEMBER VE DAİRE

ÇEMBER Ɖ Eşit uzunluktaki kirişlerin
çemberden ayırdığı yaylar S B
ve daire parçaları ve alanları
eşittir. A
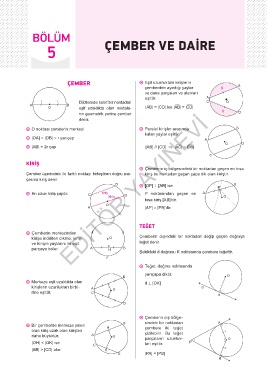
r r Düzlemde sabit bir noktadan C O
A B
O eşit uzaklıkta olan noktala- |AB| = |CD| ise |AB| = |CD|
EDİTÖR YAYINEVİ
rın geometrik yerine çember S D
denir.
Ɖ O noktası çemberin merkezi Ɖ Paralel kirişler arasında B
kalan yaylar eşittir.
Ɖ |OA| = |OB| = r yarıçap A

Ɖ |AB| = 2r çap [AB] // [CD] ⇒ |AC| = |DB| O D
C
KİRİŞ
Ɖ Çemberin iç bölgesindeki bir noktadan geçen en kısa
Çember üzerindeki iki farklı noktayı birleştiren doğru par- kiriş bu noktadan geçen çapa dik olan kiriştir.
çasına kiriş denir.
D Ɖ [OP] ^ [AB] ise P B
Ɖ En uzun kiriş çaptır. C kiriş kiriş B P noktasından geçen en A O
kısa kiriş [AB]’dir.
O
A |AP| = |PB|’dir.

TEĞET
Ɖ Çemberin merkezinden
kirişe indirilen dikme, kirişi O Çemberin dışındaki bir noktadan değip geçen doğruya
ve kirişin yaylarını iki eşit teğet denir.
parçaya böler. A H B
Şekildeki d doğrusu K noktasında çembere teğettir.
F
Ɖ Teğet, değme noktasında
yarıçapa diktir.
B O
Ɖ Merkeze eşit uzaklıkta olan d ^ [OK]
kirişlerin uzunlukları birbi- A d
rine eşittir. C O
K
D

Ɖ Çemberin dış bölge-
Ɖ Bir çemberde merkeze yakın H B sindeki bir noktadan A
çembere iki teğet
olan kiriş uzak olan kirişten r
daha büyüktür. A O çizilebilir. Bu teğet
parçaların uzunluk-
|OH| < |OK| ise ları eşittir. P O
C
|AB| > |CD| olur. K r
D |PA| = |PB|
B