Page 109 - 10. SINIF VIP TÜM DERSLER KONU ANLATIMLI - EDİTÖR YAYINLARI

ÇOK
ÇOKGENLER VE ÖZELLIKLERIGENLER VE ÖZELLIKLERI 5. ÜNITE 109
n ∈ N ve n ≥ 3 olmak üzere aynı düzlemde ardışık üç tanesi doğrusal olmayan A , A , A , A noktalarını [A A ],
1
2
2
3
1
n
[A , A ], [A , A ] şeklinde birleştirilen doğru parçalarına çokgen denir.
2 3 n 1
• A , A , , A noktalarına çokgen köşeleri denir.
2
1
n
• [A A ], [A A ], , [A A ] çokgenin kenarlarıdır. A 1 A n
n
2
1
1
2
3
• Bir çokgenin komşu olmayan iki köşesini birleştiren doğru parçası çokgenin bir A 2 çokgenin
köşesi
köşegenidir. köşegen
• Çokgenler kenar sayısına göre adlandırılır.
• Üç kenarı olan çokgen → üçgen A 3
• Dört kenarı olan çokgen → dörtgen gibi. çokgenin
EDİTÖR YAYINLARI
kenarı A 4 A 5
̛ Örnek: Aşağıda verilen geometrik şekillerden çokgen olanları belirleyelim.
A
A
Şekil doğru parçala-
Şeklin doğru parçaları rından oluşmuş ve
B D uç noktalarında kesişti- C bu doğru parçaları uç
ğinden çokgendir� noktalarından kesişti-
B D
ğinden çokgendir�
C
D D
A
A [AC] ve [BD] uç nokta-
larından farklı olarak E E Şeklin tamamı doğru
parçasından oluşmadı-
E noktasında kesiştiğin- C ğından çokgen değildir�
C den çokgen değildir�
B

A F
Çokgenin Açıları:
Bir çokgenin komşu kenarlarının oluşturduğu, çokgenin iç bölgesindeki açı-
lara iç açı, aynı köşeden geçen iki kenardan birinin uzantısıyla diğerinin B E
yaptığı açıya dış açı denir.
.
• n kenarlı bir çokgenin iç açılarının ölçüleri toplamı (n-2) 180º dir.
• n kenarlı bir çokgenin dış açılarının ölçüleri toplamı 360º dir. dış açı İç açı
C D

A B
x
130°
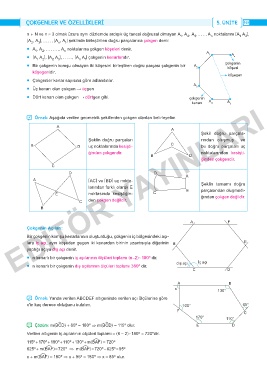
̛ Örnek: Yanda verilen ABCDEF altıgeninde verilen açı ölçülerine göre
x'in kaç derece olduğunu bulalım. 100° 65°
F C
170° 110°
̚ Çözüm: m(BëCD) + 65º = 180º ⇒ m(BëCD) = 115º olur� E D
Verilen altıgenin iç açılarının ölçüleri toplamı = (6 - 2) . 180º = 720ºdir.

115º + 170º + 100º + 110º + 130º + m(BéAF) = 720º
625º + m(BéAF) = 720º ⇒ m(BéAF) = 720º - 625º = 95º
x + m(BéAF) = 180º ⇒ x + 95º = 180º ⇒ x = 85º olur�