Page 114 - 10. SINIF VIP TÜM DERSLER KONU ANLATIMLI - EDİTÖR YAYINLARI

114

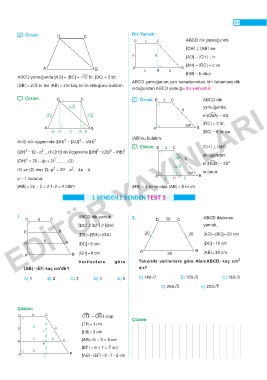
̛ Örnek: D C Dik Yamuk:
D c C ABCD dik yamuğunda
[CH] ⊥ [AB] ise
h h |AD| = |CH| = h
|AH| = |DC| = c ve
A B A c H b B
ABCD yamuğunda |AD| = |BC| = ò12 br, |DC| = 2 br, |HB| = b olup
ABCD yamuğunun yan kenarlarından biri tabanlara dik
|DB| = 2ñ5 br ise |AB| = x'in kaç birim olduğunu bulalım.
olduğundan ABCD yamuğu dik yamuktur�
̚ Çözüm: D C ̛ Örnek: D 2 C ABCD dik
EDİTÖR YAYINLARI
2ñ5 yamuğunda,
6
ò12 ò12 m(CéBA) = 60,
60º |DC| = 2 br,
A B A B
p H 2 K p |BC| = 6 br ise
|AB|'nu bulalım.
2
2
AHD dik üçgeninde |DH| = |AD| - |AH| 2
̚ Çözüm: D 2 C [CH] ⊥ [AB]
2
2
2
2
2
|DH| = 12 - p (1) DHB dik üçgeninde |DH| = |DB| - |HB| olduğundan
2
2
|DH| = 20 - (p + 2) (2) 30º 6 m(HéCB) = 30
o
2
2
(1) ve (2) den 12-p = 20 - p - 4p - 4 3ñ3 bulunur.
A 60º B
p = 1 bulunur. 2 H 3
|AB| = 2p + 2 = 2�1+2 = 4 birim |HB| = 3 birim olup |AB| = 5 br dir.
1 BENDEN 1 SENDEN TEST 3
1. ABCD dik yamuk, 2. ABCD ikizkenar
D 6 C D 10 C
[DC] // [EF] // [GH] yamuk,
E F 20
|DE| = |EG| = |GA| 20 |AD| = |BC| = 20 cm
8
G H |DC| = 6 cm |DC| = 10 cm

A B |GH| = 8 cm A 30 B |AB| = 30 cm
2
Verilenlere göre Yukarıda verilenlere göre Alan(ABCD) kaç cm
|AB| - |EF| kaç cm'dir? dir?
A) 1 B) 2 C) 3 D) 4 E) 5 A) 140ñ7 B) 160ñ3 C) 180ñ3
D) 200ñ3 E) 220ñ7

Çözüm:
D 6 C C¿TF ∼ C¿KH olup
Çözüm:
|TF| = 1 cm
6
E F
T |LB| = 3 cm
6 2 |AB| = 6 + 3 = 9 cm
G H
K
|EF| = 6 + 1 = 7 cm
6
A L B |AB| - |EF| = 9 - 7 = 2 cm