Page 17 - 10-sinif-özetli-lezzetli-matematik-22

[İKİ FONKSİYONUN BİLEŞKESİ] 75

14 A 1 A 2 A 3 17 g: → , g(x) = 2x – 1
2
3
x 2x +1 x -4 h: → , h(x) = x + 4
olduğuna göre, aşağıdakilerden hangisi
doğrudur?
f g
A) (hoh)(x) = x + 4
Yukarıdaki şekilde; x > 0 olmak üzere
B) (hog)(x) = (hoh)(x)
• Α ’den A ’ye f C) (goh)(x) = g(x + 4)

2
1
• A ’den A ’e g
2
3
fonksiyonları verilmiştir. D) (gog)(x)= (hog)(x)
E) (gog)(x) = (hoh)(x)
Buna göre (fog)(9) kaçtır?
A) 30 B) 31 C) 32 D) 33 E) 36

15 f: R → R, [fof](x) = 9x + 6
18
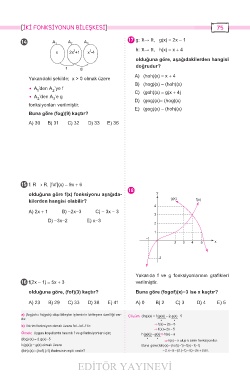
olduğuna göre f(x) fonksiyonu aşağıda- y
kilerden hangisi olabilir? g(x) f(x)
4
A) 2x + 1 B) -2x-3 C) - 3x - 3
3
D) -3x-2 E) x-3
2
1
-1
2 3 4 5 x

-2

Yukarıda f ve g fonksiyonlarının grafikleri
16 f(2x – 1) = 5x + 3 verilmiştir.
olduğuna göre, (fof)(3) kaçtır? Buna göre (fogof)(x)=3 ise x kaçtır?

A) 23 B) 29 C) 33 D) 38 E) 41 A) 0 B) 2 C) 3 D) 4 E) 5

a) (fog)oh= fo(goh) olup bileşke işleminin birleşme özelliği var- Çözüm: (fog)(x) = f (g(x)) = 2.g(x) 5
−
dır.
a
a
−
b) I birim fonksiyon olmak üzere foI=Iof=f tir. ⇒ f(a) = 2a 5
−
=
⇒ f(x) 2x 5
Örnek: Uygun koşullarda tanımlı f ve g fonksiyonları için; h(g(x)) =g(x) ⇒h(a) = a

(fog) (x) = 2.g(x) -5 a a ⇒h(x) = x olup h birim fonksiyondur.
h(g(x)) = g(x) olmak üzere Buna göre(foh)(x) −(hof)( 1) f(x) f(
− =
−−1)
− −
=
−−
+
(foh) (x) - (hof) (-1) ifadesinin eşiti nedir? =2.x 5 (2.( 1) 5) 2x 2dir.
EDİTÖR YAYINEVİ