Page 57 - 10. SINIF VIP TÜM DERSLER KONU ANLATIMLI - EDİTÖR YAYINLARI

PARÇALI FONKSIYON GRAFIKLERIARÇALI FONKSIYON GRAFIKLERI
P 2. ÜNITE 57
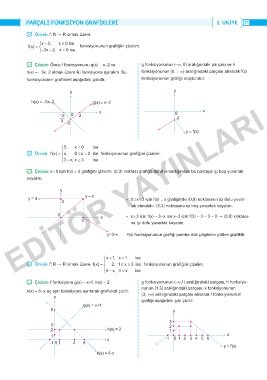
̛ Örnek: f: R → R olmak üzere

x 2 , x 0 ise
fx() fonksiyonunun grafiğini çizelim.
3 x 2 ,x 0 ise

̚ Çözüm: Önce f fonksiyonunu g(x) = x-2 ve g fonksiyonunun (-∞, 0] aralığındaki parçası ve h
h(x) = -3x-2 olmak üzere iki fonksiyona ayıralım. Bu fonksiyonunun (0, + ∞) aralığındaki parçası alınarak f(x)
fonksiyonların grafikleri aşağıdaki gibidir. fonksiyonunun grafiği oluşturulur.

y y

h(x) = −3x−2 g(x) = x−2
EDİTÖR YAYINLARI
x 0 x
−2 0 2 -2
3 -2

y = f(x)

3 , x 0 ise
x
̛ Örnek: fx() x, 0 3 ise fonksiyonunun grafiğini çizelim.

3 xx, 3 ise
̚ Çözüm: x < 0 için f(x) = 3 grafiğini çizelim. (0,3) noktası grafiğe dahil olmadığından bu noktaya içi boş yuvarlak
koyalım.

y
y = x
y = 3 • 0 ≤ x < 3 için f(x) = x grafiğinde (0,0) noktasının içi dolu yuvar-
3
lak olmalıdır. (3,3) noktasına içi boş yuvarlak koyalım.
0 x • x ≥ 3 için f(x) = 3-x ise x=3 için f(3) = 3 - 3 = 0 → (3,0) noktası-
3 na içi dolu yuvarlak koyalım.

y=3-x f(x) fonksiyonunun grafiği pembe düz çizgilerle çizilen grafiktir.

x 1 , x 1 ise
̛ Örnek: f: R → R olmak üzere fx() , 21 x 3 ise fonksiyonunun grafiğini çizelim.

6 x, 3 x ise
̚ Çözüm: f fonksiyonu g(x) = x+1, h(x) = 2 g fonksiyonunun (-∞,1) aralığındaki parçası, h fonksiyo-
nunun [1,3] aralığındaki parçası, k fonksiyonunun
k(x) = 6-x üç ayrı fonksiyona ayrılarak grafikleri çizilir. (3, +∞) aralığındaki parçası alınarak f fonksiyonunun
y
grafiği aşağıdaki gibi çizilir.
g(x) = x+1
6 y

3
3 2
2 h(x) = 2 1
1 -1 0 1 2 3 4 5 6 x
-1 0 1 4 6 x
y = f(x)
k(x) = 6-x