Page 129 - 9. SINIF MATEMATİK FAVORİ DEFTERİM

4. Ünite: Üçgenler ETKİNLİK DEFTERİ

17. İç ve Dış Açıortay Teoremi

Etkinlik Aşağıda verilen üçgenlerde istenen kenar uzunluklarını bulunuz.

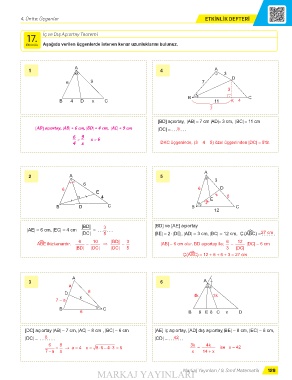
A
1 4 A
3
D
6 9 7
3
B C
B 4 D x C 11 K 4
7

[BD] açıortay, |AB| = 7 cm |AD|= 3 cm, |BC| = 11 cm
[AD] açıortay, |AB| = 6 cm, |BD| = 4 cm, |AC| = 9 cm |DC| = 5
6 9
= x = 6
4 x DKC üçgeninde, (3 - 4 - 5) özel üçgeninden |DC| = 5'tir.

A
2 A 5 3
6
6 E 6 D
. 4 k 6
2k E
B D C B C
12

|BD| 3 [BD] ve [AE] açıortay
|AE| = 6 cm, |EC| = 4 cm =
|DC| 5 |BE| = 2 . |DE|, |AD| = 3 cm, |BC| = 12 cm, Ç (A¿BC) = 27 cm
A¿BE ikizkenardır. 6 = 10 ⇒ |BD| = 3 |AB| = 6 cm olur. BD açıortay ile; 6 = 12 |DC| = 6 cm
|BD| |DC| |DC| 5 3 |DC|
Ç(A¿BC) = 12 + 6 + 6 + 3 = 27 cm

A
3 6 A
a
D 8 4k 3k
7 - a x
B C
6 B 8 E 6 C x D

[DC] açıortay |AB| = 7 cm, |AC| = 8 cm , |BC| = 6 cm [AE] iç açıortay, [AD] dış açıortay,|BE| = 8 cm, |EC| = 6 cm,
|DC| = 6 |CD| = 42
6 = 8 → a = 4 x = 8 6 43 ⋅ = 6 3k = 4k ise x = 42
⋅-
7a a x 14 + x
-

Markaj Yayınları / 9. Sınıf Matematik
MARKAJ YAYINLARI 129