Page 132 - 9. SINIF MATEMATİK FAVORİ DEFTERİM

ETKİNLİK DEFTERİ 4. Ünite: Üçgenler

20. Dik Üçgende Öklid ve Pisagor Teoremi

Etkinlik Aşağıda verilen şekillerde istenen kenar uzunluklarını bulunuz.

A
1 x 4
D
A
17
4

B 9 11 H 2 D 7 C
B
8 C
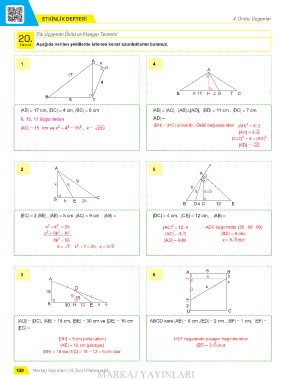
|AB| = 17 cm, |DC| = 4 cm, |BC| = 8 cm |AB| = |AC|, [AB]⊥[AD], |BD| = 11 cm , |DC| = 7 cm

8, 15, 17 üçgeninden |AD| =
.
2
2
2
2
|AC| = 15 cm ve x + 4 = 15 , x = 209 |BH| = |HC| olmalıdır. Öklid bağıntısından |AH| = 9 2
|AH| = 3ñ2
2
(3ñ2) + 4 = |AD| 2
|AD| = ò22
2 A 5
A
9
x 5 x
8 4ñ3
B k E 2k C
B D 4 C 12 E

|EC| = 2.|BE| , |AE| = 5 cm ,|AC| = 9 cm |AB| = |DC| = 4 cm, |CE| = 12 cm, |AB| =

.
2
2
2
x + k = 25 |AC| = 12 4 ADC üçgeninde (30 - 60 - 90)
2
2
x + 9k = 81 |AC| = 4ñ3 |BD| = 8 olur.
2
8k = 56 |AD| = 8'dir. x = 8ñ3'dür.
2
k = ñ7 x + 7 = 25, x = 3ñ2
3 6 A 1 6 B
6
1
A H
F
D 3 x
18
9 15
B 30 H 12 E x C E
2
D C
|AD| = |DC|, |AB| = 18 cm, |BE| = 30 cm ve |DE| = 15 cm ABCD kare |AB| = 6 cm ,|ED| = 2 cm , |BF| = 1 cm, |EF| =
|EC| =
|DH| = 9 cm (orta taban) HEF üçgeninde pisagor bağıntısından
|HE| = 12 cm (pisagor) |EF| = 3ñ5 olur.
|BH| = 18 ise |EC| = 18 - 12 = 6 cm olur.

132 Markaj Yayınları / 9. Sınıf Matematik
MARKAJ YAYINLARI