Page 126 - 9. SINIF MATEMATİK FAVORİ DEFTERİM

ÖZETİN ÖZETİ 4. Ünite: Üçgenler

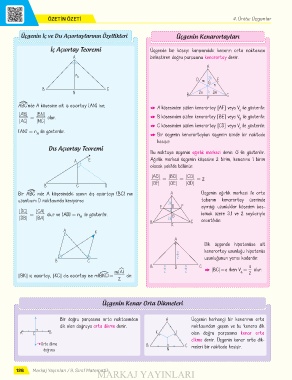
Üçgenin İç ve Dış Açıortaylarının Özellikleri Üçgenin Kenarortayları

İç Açıortay Teoremi Üçgende bir köşeyi karşısındaki kenarın orta noktasına
A birleştiren doğru parçasına kenarortay denir.
A
n
A 2k
D m E
G n
B C
N B 2n k 2m C
F
A¿BC’nde A köşesine ait iç açıortay [AN] ise; Q A köşesinden çizilen kenarortay [AF] veya V ile gösterilir.
a
|AB| = |BN| olur. Q B köşesinden çizilen kenarortay [BE] veya V ile gösterilir.
|AC| |NC| b
Q C köşesinden çizilen kenarortay [CD] veya V ile gösterilir.
c
[AN] = n ile gösterilir.
A Q Bir üçgenin kenarortayları üçgenin içinde bir noktada
kesişir.
Dış Açıortay Teoremi
Bu noktaya üçgenin ağırlık merkezi denir. G ile gösterilir.
A E Ağırlık merkezi üçgenin köşesine 2 birim, kenarına 1 birim
olacak şekilde bölünür.
|AG| = |BG| = |CG| = 2
|GF| |GE| |GD|
B C D
Bir A¿BC nde A köşesindeki açının dış açıortayı [BC] nın A Üçgenin ağırlık merkezi ile orta
uzantısını D noktasında kesiyorsa 3k tabanın kenarortay üzerinde
E D F ayırdığı uzunluklar köşeden baş-
|DC| = |CA| olur ve [AD] = n ile gösterilir. k lamak üzere 3,1 ve 2 sayılarıyla
|DB| |BA| A 2k G
B C orantılıdır.
K
A K
A
Dik üçgende hipotenüse ait

a kenarortay uzunluğu hipotenüs
2 uzunluğunun yarısı kadardır.
B C
B a D a C a
m(ëA) 2 2 Q |BC| = a iken V = olur.
a
2
[BK] iç açıortay, [KC] dış açıortay ise m(BéKC) = dir.
2

Üçgenin Kenar Orta Dikmeleri

Bir doğru parçasına orta noktasından A Üçgenin herhangi bir kenarının orta
dik olan doğruya orta dikme denir. noktasından geçen ve bu kenara dik
A C B K l olan doğru parçasına kenar orta
dikme denir. Üçgenin kenar orta dik-
Orta dikme B C meleri bir noktada kesişir.
doğrusu N

MARKAJ YAYINLARI
126 Markaj Yayınları / 9. Sınıf Matematik