Page 83 - 10. SINIF VIP TÜM DERSLER KONU ANLATIMLI - EDİTÖR YAYINLARI
P. 83
POLINOMLARIN ÇARPANLARA AYRILMASI VE ÖZDEŞLIKLERINOMLARIN ÇARPANLARA AYRILMASI VE ÖZDEŞLIKLER
POL 3. ÜNITE 83
• Bir polinomun iki ya da daha fazla polinomun çarpımı biçiminde yazılması işlemine çarpanlara ayırma denir.
• P(x), Q(x) ve R(x) birer polinom olmak üzere;
R(x) = P(x) . Q(x) eşitliğinde P(x) ve Q(x) polinomlarına R(x) polinomunun çarpanları denir.
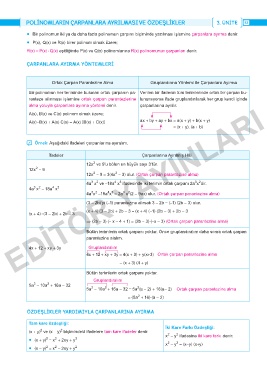
ÇARPANLARA AYIRMA YÖNTEMLERI
Ortak Çarpan Parantezine Alma Gruplandırma Yöntemi ile Çarpanlara Ayırma
Bir polinomun her teriminde bulunan ortak çarpanın pa- Verilen bir ifadenin tüm terimlerinde ortak bir çarpan bu-
ranteze alınması işlemine ortak çarpan parantezlerine lunamıyorsa ifade gruplandırılarak her grup kendi içinde
EDİTÖR YAYINLARI
alma yoluyla çarpanlara ayırma yöntemi denir. çarpanlarına ayrılır.
A(x), B(x) ve C(x) polinom olmak üzere;
A(x) . B(x) + A(x) C(x) = A(x) [B(x) + C(x)] ax + by + ay + bx = a(x + y) + b(x + y)
= (x + y) � (a + b)
̛ Örnek: Aşağıdaki ifadeleri çarpanlarına ayıralım.
Ifadeler Çarpanlarına Ayrılmış Hâli
2
12x ve 9'u bölen en büyük sayı 3'tür.
2
12x - 9
2
2
12x - 9 = 3(4x - 3) olur� (Ortak çarpan parantezine alma)
3
3 2
2
4
3
4a x ve -18a x ifadesinde iki terimin ortak çarpanı 2a x dir.
3 2
4
4a x - 18a x 3
3
2
3 2
4 3
4a x -18a x = 2a x (2 - 9ax) olur� (Ortak çarpan parantezine alma)
(3 - 2b)'yi (-1) parantezine alırsak 3 - 2b = (-1) (2b - 3) olur�
.
(x + 4) (3 - 2b) + 2b - 3 (x + 4) (3 - 2b) + 2b - 3 = (x + 4) (-1) (2b - 3) + 2b - 3
⇒ (2b - 3) (- x - 4 + 1) = (2b - 3) (-x - 3) (Ortak çarpan parantezine alma)
Bütün terimlerin ortak çarpanı yoktur. Önce gruplandıralım daha sonra ortak çarpan
parantezine alalım.
4x + 12 + xy + 3y Gruplandıralım
4x + 12 + xy + 3y = 4(x + 3) + y(x+3) Ortak çarpan parantezine alma
= (x + 3) (4 + y)
Bütün terimlerin ortak çarpanı yoktur.
Gruplandıralım
3
2
5a - 10a + 16a - 32
2
2
3
5a - 10a + 16a - 32 = 5a (a - 2) + 16(a- 2) Ortak çarpan parantezine alma
2
= (5a + 16) (a - 2)
ÖZDEŞLIKLER YARDIMIYLA ÇARPANLARINA AYIRMA
Tam kare özdeşliği:
İki Kare Farkı Özdeşliği:
2
2
(x + y) ve (x - y) biçimindeki ifadelere tam kare ifadeler denir. 2 2
• (x + y) = x + 2xy + y 2 x - y ifadesine iki kare farkı denir.
2
2
2
2
• (x - y) = x - 2xy + y 2 x - y = (x-y) (x+y)
2
2